In how many ways, counting ties, can eight horses cross the finishing line?
(For example, two horses, A and B, can finish in three ways: A wins, B wins, A and B tie.)
Hint - Answer - Solution
In ![]() ABC, draw AD, where D is the midpoint of BC.
ABC, draw AD, where D is the midpoint of BC.
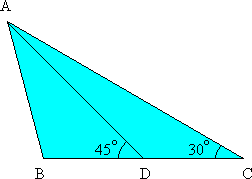
If ![]() ACB = 30° and
ACB = 30° and ![]() ADB = 45°, find
ADB = 45°, find ![]() ABC.
ABC.
Hint - Answer - Solution
A sequence of integers is defined by
Is there a value of p such that the sequence consists entirely of prime numbers?
Hint - Answer - Solution
If the equation x4 − x3 + x + 1 = 0 has roots a, b, c, d, show that 1/a + 1/b is a root of x6 + 3x5 + 3x4 + x3 − 5x2 − 5x − 2 = 0.
Hint - Solution
The minute hand of a clock is twice as long as the hour hand. At what time, between 00:00 and when the hands are next aligned (just after 01:05), is the distance between the tips of the hands increasing at its greatest rate?
Hint - Answer - Solution
Point P lies inside ![]() ABC, and is such that
ABC, and is such that ![]() PAC = 18°,
PAC = 18°, ![]() PCA = 57°,
PCA = 57°, ![]() PAB = 24°, and
PAB = 24°, and ![]() PBA = 27°.
PBA = 27°.

Show that ![]() ABC is isosceles.
ABC is isosceles.
Hint - Solution
Observe that
Are there any other primes p such that (p − 1)! + 1 is a power of p?
Hint 1 - Hint 2 - Answer - Solution
Find all positive real numbers x such that both ![]() + 1/
+ 1/![]() and
and ![]() + 1/
+ 1/![]() are integers.
are integers.
Hint - Answer - Solution
The towns of Alpha, Beta, and Gamma are equidistant from each other. If a car is three miles from Alpha and four miles from Beta, what is the maximum possible distance of the car from Gamma? Assume the land is flat.
Hint - Answer - Solution
The smallest distance between any two of six towns is m miles. The largest distance between any two of the towns is M miles. Show that M/m ![]()
![]() . Assume the land is flat.
. Assume the land is flat.
Hint - Solution