Nick's Mathematical Puzzles: 121 to 130

121. Integer sequence

The terms of a sequence of positive integers satisfy a_n+3 = a_n+2(a_n+1 + a_n), for n = 1, 2, 3, ... .

If a₆ = 8820, what is a₇?

Hint  -  Answer  -  Solution

122. Powers of 2 and 5

If the numbers 2ⁿ and 5ⁿ (where n is a positive integer) start with the same digit, what is this digit? The numbers are written in decimal notation, with no leading zeroes.

Hint  -  Answer  -  Solution

123. Right angle and median

Let ABC be a triangle, with AB AC. Drop a perpendicular from A to BC, meeting at O. Let AD be the median joining A to BC. If OAB = CAD, show that CAB is a right angle.

Triangle ABC, with perpendicular AO and median AD, as described above.

Hint  -  Solution

124. The ladder

A ladder, leaning against a building, rests upon the ground and just touches a box, which is flush against the wall and the ground. The box has a height of 64 units and a width of 27 units.

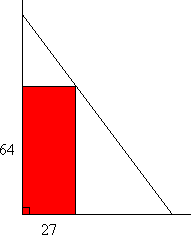
Ladder, resting against wall, and just touching box of height 64 units and width 27 units.

Find the length of the ladder so that there is only one position in which it can touch the ground, the box, and the wall.

Hint  -  Answer  -  Solution

125. Divisibility by 446617991732222310

Show that, for all integers m and n, mn(m⁴²⁰ − n⁴²⁰) is divisible by 446617991732222310.

Hint  -  Solution

126. Intersecting squares

The sides of two squares (not necessarily of the same size) intersect in eight distinct points: A, B, C, D, E, F, G, and H. These eight points form an octagon. Join opposite pairs of vertices to form two non-adjacent diagonals. (For example, diagonals AE and CG.) Show that these two diagonals are perpendicular.

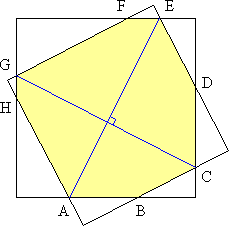
Intersecting squares, as described above, with diagonals AE and CG.

Hint  -  Solution

127. Prime number generator

Let P = {p₁, ... , p_n} be the set of the first n prime numbers. Let S be an arbitrary (possibly empty) subset of P. Let A be the product of the elements of S, and B the product of the elements of S', the complement of S. (An empty product is assigned the value of 1.)

Prove that each of A + B and |A − B| is prime, provided that it is less than p_n+1² and greater than 1.

For example, if P = {2, 3, 5, 7}, the table below shows all the distinct possibilities for A + B and |A − B|. Values of A + B and |A − B| that are less than p₅² = 121 and greater than 1, shown in bold, are all prime.

Prime number generator example
S	S'	A	B	A + B	\|A − B\|
Empty set	{2, 3, 5, 7}	1	210	211	209
{2}	{3, 5, 7}	2	105	107	103
{3}	{2, 5, 7}	3	70	73	67
{5}	{2, 3, 7}	5	42	47	37
{7}	{2, 3, 5}	7	30	37	23
{2, 3}	{5, 7}	6	35	41	29
{2, 5}	{3, 7}	10	21	31	11
{2, 7}	{3, 5}	14	15	29	1

Hint  -  Solution

128. Modular equation

For how many integers n > 1 is x⁴⁹ x (modulo n) true for all integers x?

Hint  -  Answer  -  Solution

129. Abelian group

Let G be a group with the following two properties:

(i) For all x, y in G, (xy)² = (yx)²,
(ii) G has no element of order 2.

Prove that G is abelian.

Hint  -  Solution

130. Reciprocal polynomial?

Let p be a polynomial of degree n with complex coefficients. Is there a value of n such that the equations

p(1) = 1/1,
p(2) = 1/2,
...
p(n) = 1/n,
p(n + 1) = 1/(n + 1),
p(n + 2) = 1/(n + 2),

can be satisfied simultaneously?

Hint  -  Answer  -  Solution